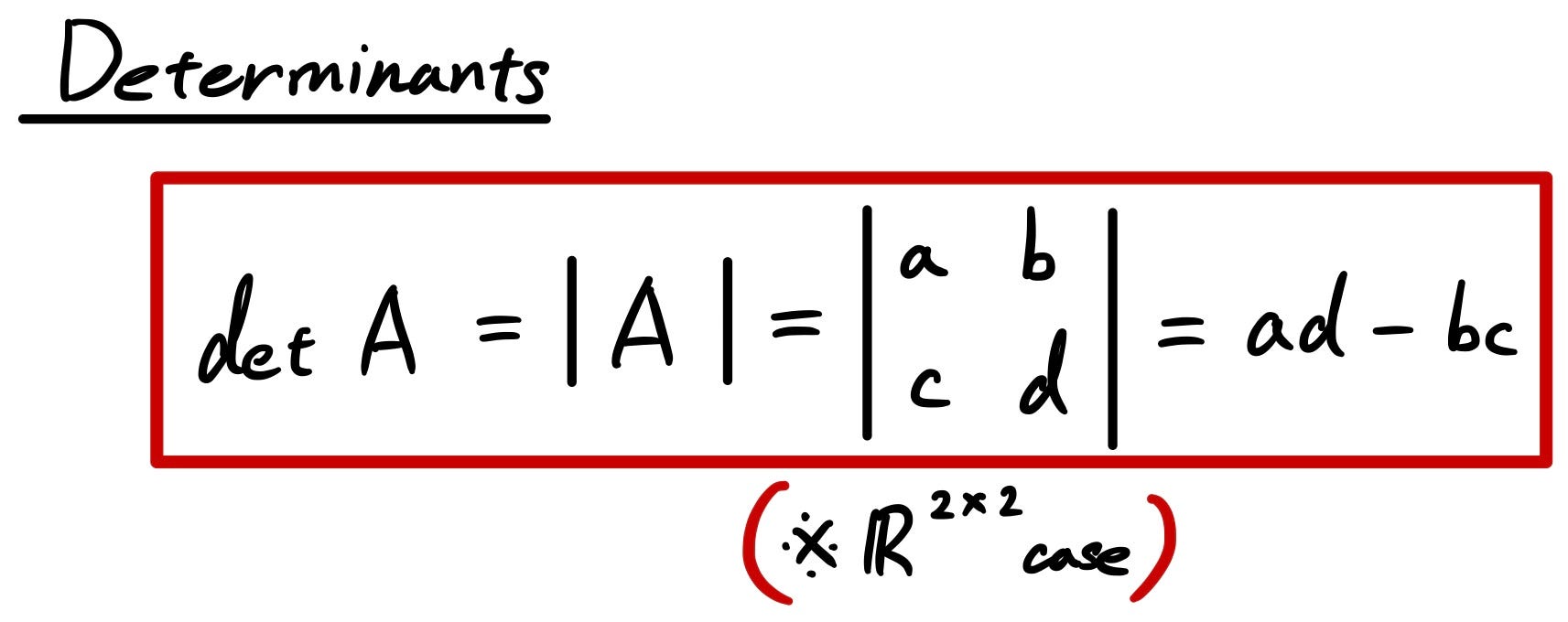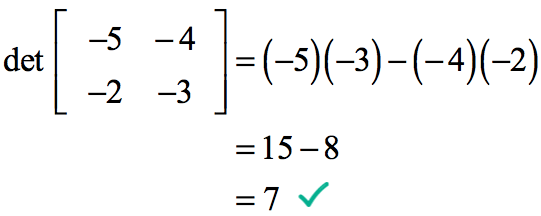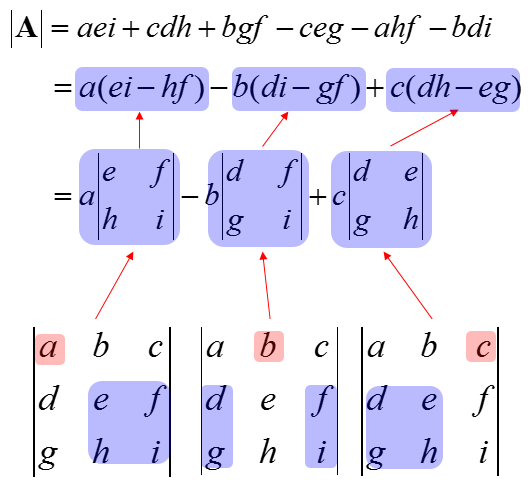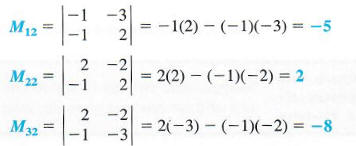Determinants are used to solve the eigenvalue equation determinants are used to find the volume form of a riemannian space determinants are used to guarantee the invertibility of matrix groups determinants are used to check whether the bijectivity of a diffeomorphism jul 29 2003 4.
What is a matrix determinant used for.
The most obvious use you may find is indirect within broader procedures like the degree of a non square matrix linear in dependence linear systems and so on.
The determinant is useful for solving linear equations capturing how linear transformation change area or volume and changing variables in integrals.
The determinant of a matrix gives information about how the associated linear transformation changes the area volume of a unit square cube hypercube.
Det a 1 1 det a.
The selection of the topic determinant of a matrix is a bit too narrow to be directly used in real world uses.
The determinant helps us find the inverse of a matrix tells us things about the matrix that are useful in systems of linear equations calculus and more.
However i have rarely had a practical need to compute volumes using determinants.
A matrix is an array of many numbers.
Multiply the main diagonal elements of the matrix determinant is calculated.
I find this interpretation to be the most intuitive and many standard results for determinants can be understood using this viewpoint.
The determinant also gives the signed volume of the parallelepiped whose edges are the rows or columns of a matrix.
For a square matrix i e a matrix with the same number of rows and columns one can capture important information about the matrix in a just single number called the determinant.
Determinants occur throughout mathematics.
For example a matrix is often used to represent the coefficientsin a system of linear equations and the determinant can be used to solvethose equations although other methods of solution are much more computationally efficient.
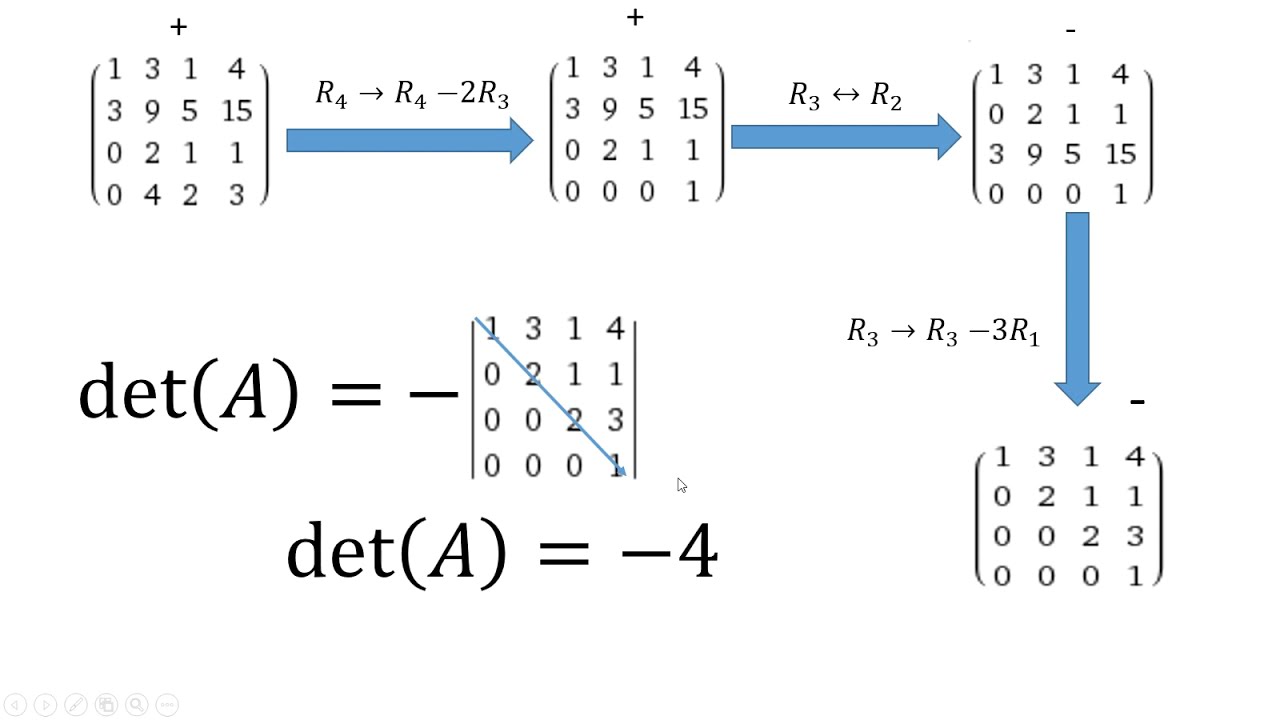
Reduce this matrix to row echelon form using elementary row operations so that all the elements below diagonal are zero.
Determinants can be used to solve linear systems using cramer s rule where the division of the determinants of two related square matrices equates to the value of each of the system s variables.
You can know a few things with it.
The determinant of a matrix.
When the determinant is zero the transformation collapses the cube into a lower dimensional subspace and the associated transformation is non invertible.